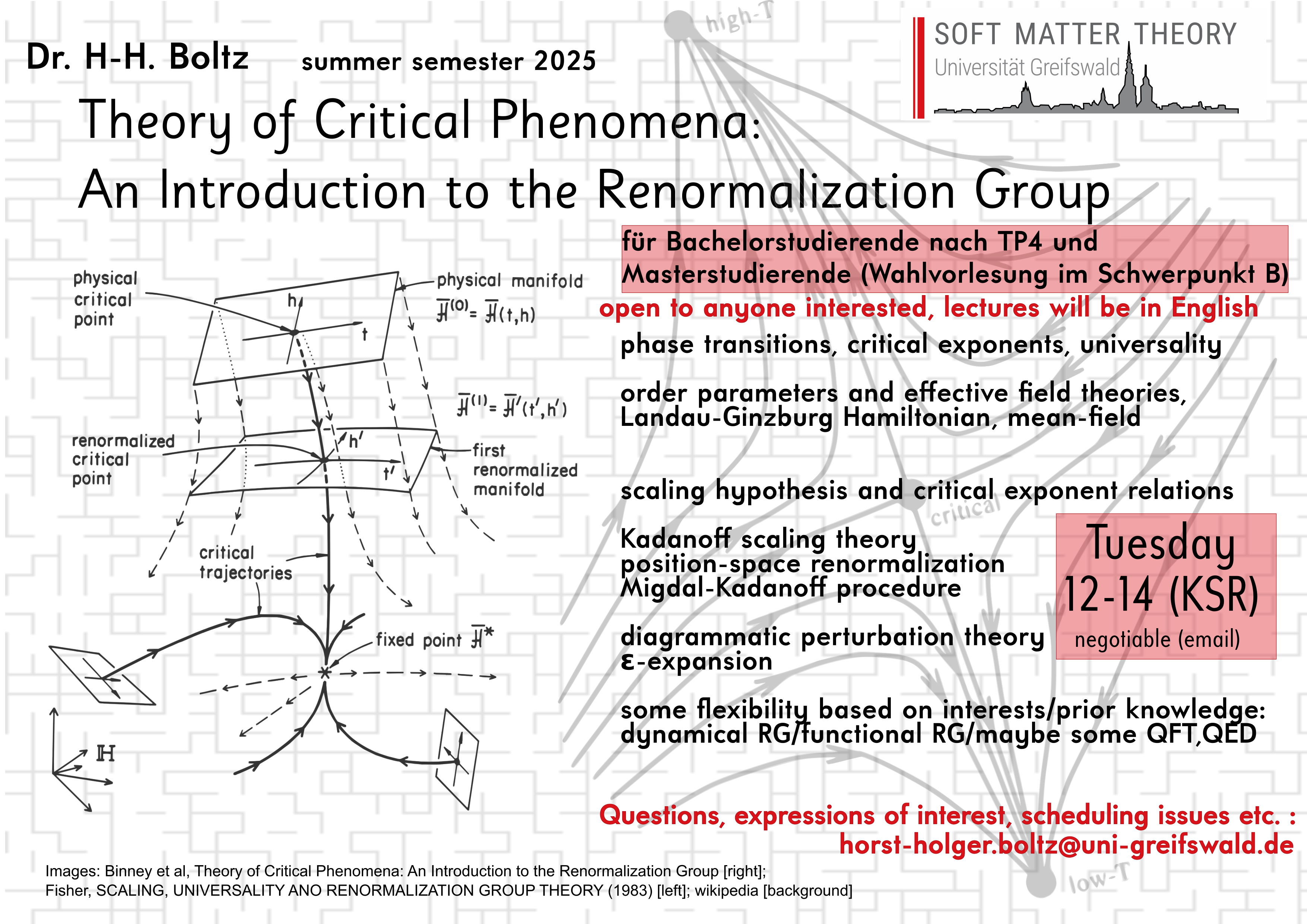
An introduction into the theory of critical phenomena beyond introductory statistical mechanics classes with a particular focus to renormalization methods.
This lecture is planned as a rather gentle introduction into some advanced and still very active concepts in statistical physics. It is intended for students of physics who have taken a first statistical physics course (e.g. TP4). There are no other prerequisites (particularly no knowledge in quantum field theory is assumed). As most of the literature is in English, the lecture will be as well (unless there is a unanimous vote to the contrary).
Given interest, there is plenty of room for optional excercise problems (numerical and analytical).
Topics: (Continuous) Phase transitions, order parameters and correlation functions, critical exponents and scaling, Universality
as necessary: introduction to some relevant model systems (Ising, percolation, XY and Heisenbergmodel, Potts mdodel, Gaussian and spherical models)
Mean-Field theory, Landau(-Ginzburg) theory
Real-space renormalization: block-spin RG, RG exponents
possibly: diagrammatic perturbation theory
momentum shell RG, epsilon-expansion, upper/lower critical dimension, universality revisited
depending on time/interest: dynamical RG (for example toner-tu theory), functional ("exact") RG, maybe some QFT/QED
- Dozent/in: Horst-Holger Boltz
- Dozent/in: Thomas Ihle